Poetic Phi

Artists across generations have been looking to nature as inspiration for their work. This includes painting, photography, symphonies, and poetry. However, what many artists fail to realize is that looking to mathematics can lead to similar motivation. In fact, a lot of the patterns seen in our natural world, and even the vast outer space beyond the earth, originate from mathematics.

‘Pure mathematics is, in its way, the poetry of logical ideas.’ ~Albert Einstein

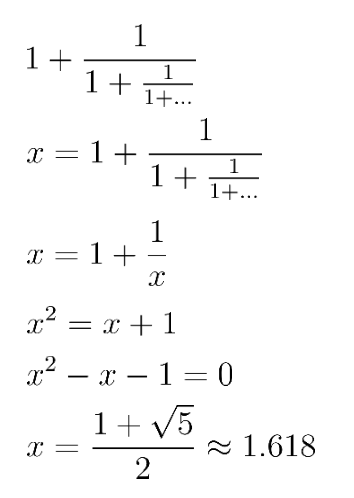
One of the most common types of patterns originates from phi (Φ). This value is equal to the first infinite fraction that we see on the right, but because it repeats infinitely, it seems almost impossible for us to be able to calculate such a value. However, a simple but creative use of algebraic substitution allows us to exploit the issue of infinite repetition and calculate our answer!

Also, yay, my LaTeX skills have gotten so much better.

The above derivation is probably the coolest part of all the math, so I'll skip the rest of the math and simply mention (proof left as an exercise to the reader) that from this polynomial, we can arrive at the well-known Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, ... (each number is the sum of the 2 numbers before it). A visualization of this sequence gives us the Golden Spiral (Φ is also known as The Golden Ratio).

The Golden Ratio is often explained using the ratio

of the side lengths of the above Golden Rectangle.

In case anyone didn't follow some of the math, we essentially used Φ to derive from the infinitely repeating fraction, we've derived an infinite sequence that is visualized in a repetitive spiral. Much like poetry, the spiral keeps the same central pattern, but continues building off of it over time.

Spiraling back to the topic of math in nature, researchers have found numerous instances of the Golden Spiral. Here's a few of these findings:

I couldn't find images of these instances, but research papers reported the Golden Spiral being additionally present in:

• magnetic resonance of spins in cobalt niobate crystals

• number of veins in a leaf

• dimensions of Giza pyramid